Are connectionist models neurally plausible? A critical appraisal
PAPADATOU-PASTOU M.
Dr. Research Centre for Psychophysiology and Education, National and Kapodistrian University of Athens, e-mail: mpapadatou@primedu.uoa.gr

"Our goal in short is to replace the computer metaphor with the brain metaphor."
(Rumelhart, 1989, p.134)

Encephalos 2011, 48(1):5-12.

FULL TEXT IN PDF FORMAT

Introduction

In the 1980s a new type of cognitive model began to receive increasing attention in the neuroscience literature, with the explosion of interest reaching its peak in 1986 when Rumelhart, McClelland, and the PDP Research Group released the locus classicus of connectionism “Parallel Distributed Processing”.  These new models became variously known under different names such as connectionist models or networks, parallel distributed processing models, or artificial neural networks.  The latter term is indicative of the fact that connectionism is inspired by information processing in the brain and attempts to capture the essential computational properties of the real neuronal elements found in the central nervous system using simulations of smaller networks of more abstract units (Plaut et al., 1996; O’Reilly, 1998; Engelbrecht, 2007).

A connectionist model typically consists of a large number of processing units - closely analogous to abstract neurons or groups of neurons - joined together in a multi-layer pattern of parallel connections. The units are usually segregated into three classes: input units, which receive information to be processed (i.e., the stimulus presented to the model), output units, where the results of the processing are to be found (i.e., the model’s response), and units in between called hidden units (Fig.1). Each unit sums up information from units in the previous layer, performs a simple computation on this sum and passes the result to units in the next layer. The influence of a unit in one layer on a unit in the next layer depends upon the weight or the strengths of the connections between units. Connections can be excitatory or inhibitory – inhibitory connections decrease the activation of the receiving node, whereas excitatory connections increase the receiving node’s activity level.  Learning to produce the correct output in response to a given input is achieved by changing the strength of connections between the units until the network settles into a stable pattern (for a more detailed description of the architecture of connectionist networks see McLeod et al., 1998; O’Reilly & Munakata, 2000; Heinke & Mavritsaki, 2009).

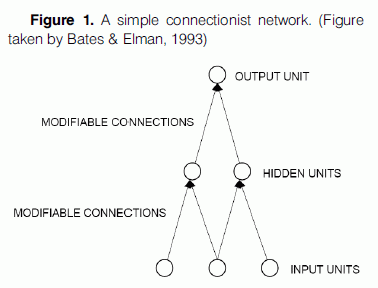
The most appealing aspect of the connectionist approach lies in the fact that it starts with a model that incorporates brain-like processing and sees whether behaviour, which mimics that shown by people, emerges. That is, connectionist models actually produce a response to a stimulus, making it possible to compare at a quantitative level the predictions that the models make to the behaviour produced by participants in empirical studies. For example, a model of reading aloud takes time to generate a response and this varies with the frequency of the word (McLeod et al., 1998). If the predictions are wrong the model fails and vice versa. This is obviously not the case for the traditional box-and-arrow models of cognitive processes, which allow only for qualitative predictions. In the case of artificial intelligence models, modeling of the human cognitive capacities is possible, but no attempt is made to relate the operations performed to the way the brain works in a neuronal level.

Despite the parallels to biological systems, the neural plausibility of connectionist models has been widely argued. The central principles of connectionist models are in actual fact derived from our current knowledge of computation within the brain, so the models are justly said to be neurally inspired (McLeod et al., 1998; Barber & Kuts, 2007). On the other hand, it is also true that connectionist networks do not replicate all known features of the brain (Seidenberg & Zevin, 2006), or/and they contain mechanisms that are biologically or neurologically unrealistic or downright false (Morris, 1989; Roy, 2000). One skeptic has gone even further, claiming that “the only thing neural networks have in common with the human brain is the word ‘neural’ ” (Poggio, 1988).

It looks like the “brain-like structure of connectionist architectures” (Clark, 1989) may not be as straightforward as it initially appears. Without appropriate qualification, the claims about elements which have been termed “brain-like” or “neural-like” have a great potential to mislead. These claims form the basis of every attempt to simulate cognitive processes using connectionist modeling. This being the case, it is of great interest and methodological importance to investigate the claims raised by connectionism in a careful manner.

Processing units-neurons

Let us begin by examining the claim that “a connectionist processing unit is something close to an abstract neuron” (Rumelhart, 1989). This claim has aroused a lot of dispute, since “it has always been very clear to neuroscientists that there is no such thing as a typical neuron” (Winlow, 1990). As a matter of fact, twelve different kinds of neurons are to be found in the neocortex alone, according to Churchland and Sejnowski (1994). It is only sensible that Berkeley (1997) wonders, “just which kind of neuron connectionist processing units are an abstraction from?” Since the “abstract neurons” employed in connectionist networks are supposed to capture the significant features of all neurons, Berkeley further wonders how were the selected set of features decided upon.

Connectionists acknowledge the fact that there are many different types of neurons, but they claim that despite the neurons’ bewildering variety in detail, they perform a common function which is to intergrate information about the firing of one set of neurons (their input) and pass information related to this input (their output) to a new set of neurons. This operation takes place in three different stages: first, the neuron receives signals, either excitatory or inhibitory from other neurons, via synaptic connections onto its dendrites. If the sum of these signals exceeds a threshold, the neuron fires and this is communicated to other neurons by a signal passing down its axon. This signal in turn acts as part of the input to the dendrites of other neurons.

Connectionist models consist of a number of units that behave in exactly the same way. As shown in Figure 2, each line coming into the unit from above represents an input connection, which may be either positive or negative. The unit sums the inputs and passes information about the sum down the output connections to other units to which it is connected. Therefore “the functional role of a unit in a connectionist model is the same as that of a classical neuron” (McLeod et al., 1998), as they both pass information about the pattern of activity of one set of units to another set (Crick & Asanuma, 1986). Still, neurons in the brain are not only highly recurrent (“loops within loops”) but sparsely connected, they also have accidental features in their connectivity patterns (Maass et al., 2002).

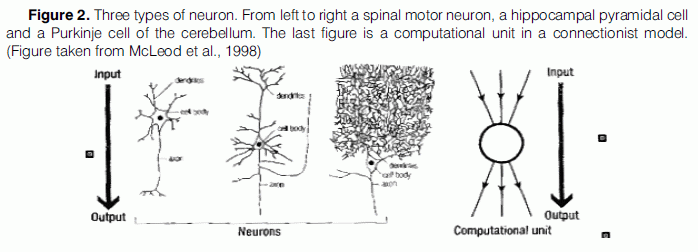
A related concern to neuronal diversity derives from the fact that many, if not most, connectionist models include what is known as a “bias” term, which is trained at the same time as the connection weights are trained. Its role is to add a constant amount to the net input computed by the output unit. Typically all units in a network will receive input from the bias unit. However, there is little or no evidence that the most natural biological equivalents of bias, the threshold membrane potentials, can be similarly modified (Berkeley, 1997). Thus, it seems that connectionists take it upon themselves to add an extra degree of freedom into their networks - yet this degree of freedom lacks any biological justification or defence argument from the connectionist point of view.

Signal transmission

Berkeley, among others, does not consent to this being the case and he gives five reasons to back up his claim (1997). Firstly, he argues that different types of neurons have different firing patterns. Secondly, the firing patterns of some neurons are a function of their recent firing history. Thirdly, some neurons have oscillatory firing patterns. Fourthly, most neurons spike randomly, even in the absence of input (Churchland & Sejnowski, 1994; Maass et al., 2002). Finally, signals between neurons in biological systems are sent by more than one medium –synaptic transmission occurs by both electrical and chemical means (Getting, 1989). Although it may be possible to capture at least some aspects of these complexities with continuous values, Berkeley is sceptical whether this can be entirely the case. He believes that there must be at least some functionally significant properties of the biological systems that are not captured in connectionist arguments, even though he clearly avoids being more specific as to name which mechanisms are not captured.

An additional issue that needs to be examined is the relationship between the signal that is transmitted and the influence it has upon the receiving neuron, that is whether it makes it more or less likely to fire. Dreyfus (1992) briefly describes the work by Lettvin (1991), which suggests that axon branches may serve to act as “low pass filters with different cut-off frequencies”, with the precise frequency being dependent upon the physical diameter of the actual axon branch. Thus, there should be a complex and functionally significant relationship between the frequency and pattern of neuronal firing and the length and diameter of the connections between neurons. However, there is nothing in connectionist systems that is even remotely similar to such a mechanism. Moreover, extrasynaptic neuromodulators also affect synaptic adjustments in a way that can be claimed to be direct (Levine, 1991), while mechanisms within the cell convert these signals to long-lasting cellular properties. Thus, connectionist notions that no other physical entity directly signals changes to a cell’s behaviour is another misconception about the brain.

It is also the case that in standard connectionist networks individual units from one layer can have a significant impact on the activation level of particular units in the next layer. In biological systems, however, the influence of one neuron upon the state of another is relatively weak, usually in the order of 1% - 5% of the firing threshold (Churchland & Sejnowski, 1994).  Connectionists overcome these arguments by refusing to look at the biological system in such detail –they try to model a brain-like style of processing, but it is not their intention to simulate every specific detail of the brain (Plaut & McClelland, 2010; Read et al., 2010). In the case of this relationship between the signal that is transmitted and the influence it has upon the receiving neuron, they argue that this is represented directly in connectionist models. Namely, the effect that one unit has on another is determined by the strength of the connection between them, that is the weight of the connection.

Representations’ distribution

A different property that connectionist models putatively share with real neural networks is the fact that they use distributed representations (e.g., McClelland & Rogers, 2003; Conrey et al., 2007). According to O’Reilly and Farah (1999) evidence for the brain’s use of distributed representation comes from observations such as the relatively global effects of damage to a given functional area. For example, recognition of all faces is affected in prosopagnosia, not just some. Other observations are the graceful nature of degradation (i.e., tissue loss may cause only mild or moderate impairments) as well as more direct single-cell recordings. As a matter of fact, in a number of domains of processing such as motor systems and facial recognition, analyses of cells’ breadth of tuning and proportion of active cells suggests that distributed representation is ubiquitous in the brain (Desimone & Ungerleider, 1989; Georgopoulos, 1990; Sparks & Mays, 1990).

The above argument is rather problematic. Burton and Young (1999) claim that there are many ways in which representations can be distributed. Thus, in order to use the fact that a connectionist network has distributed representations as evidence that it is brain-like, one needs to argue that the particular type of distributed representations it uses is like the particular type of distributed representation the brain uses. Furthermore, most of the evidence presented suggests the use of coarse coding by the brain, not fully distributed representations. In essence this means that each representation is coded over a small proportion of the available units, rather than each being coded equally across the entire system, like typical connectionist networks would do. This is an important distinction, since systems that use “few-unit”, coarse coded distributed representations behave entirely unlike systems in which all units are used for each representation. This again mitigates against the tenability of connectionist claims to biological realism.

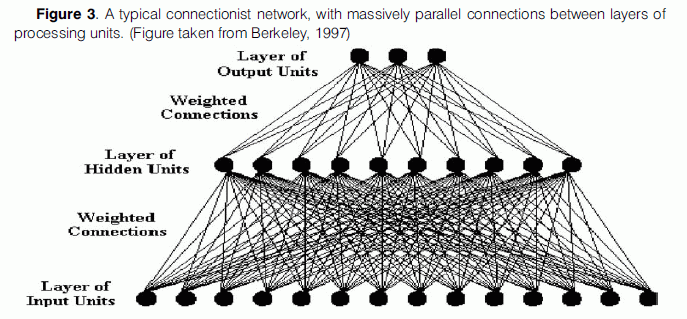
More scepticism against connectionist networks comes from the fact that they are “massively parallel”, that is each unit of a particular layer is normally arranged so that it has connections to every unit of both prior and subsequent layers in the network (Fig. 3). However, there is evidence that suggests that this is not the case in the brain and that neurons are rather sparsely connected, as stated above. Churchland and Sejnowski (1994) in their discussion about the patterns of connectivity found in brain cortex, note that “not everything is connected to everything else. Each cortical neuron is connected to a roughly constant number of neurons, irrespective of brain size, namely about 3% of the neurons underlying the surrounding millimetre of cortex”. Standard connectionist models pay no heed to this particular fact about neural systems.

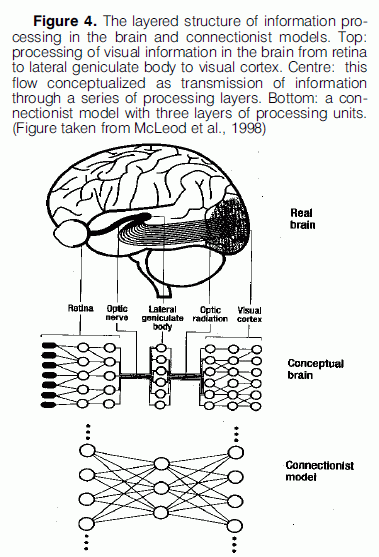
An argument that connectionists use to support their claim of modeling the global features of the cognitive processes that take place in the brain, is that connectionist models, just like the brain structure, are layered. Information is processed in the brain by a flow of activity passing through a sequence of physically independent structures. This view of the organisation processing in the brain is represented in connectionist models. Figure 4 provides an illustration of this kind of layered processing that takes place in the brain in the case of visual perception and how it is modeled by a connectionist network.

Information learning

Another area of controversy lies in the way that connectionist networks learn new information. Although the mechanisms by which the brain learns are not fully understood, there is good evidence that learning involves changing the strength of synaptic connections between neurons. In connectionist networks this mechanism is represented directly by changing the weight of connections between neurons in order for learning to be achieved. One of the most widely used training methods is called backpropagation (e.g., Gers et al., 2000; O’Reilly & Frank, 2007; Monaghan, 2008). To use this method one needs a training set consisting of many examples of input and their desired outputs for a given task. The weights of the connections are initially set to random values and then the members of the training set are repeatedly exposed to the network.

The values for the input of a member are placed on the input weight and the output of the net is compared with the desired output for this member. Then all weights in the net are adjusted slightly in the direction that would bring the net’s output values closer to the values for the desired output. After many repetitions of this process the net may learn to produce the desired output for each input in the training set.

Backpropagation has attracted the most criticism against the biological plausibility of connectionist networks. The reason is that it requires error information to be propagated backwards through the network. In a biological system this would correspond to signals traveling back down the nerve and “there is no evidence that synapses can be used in the reverse direction” (Hinton & Anderson, 1989). According to the same authors, it is also clear that real neurons cannot both propagate an error derivative backwards using a linear input-output function whilst having to propagate activity forwards using non-linear processes. This seems far more problematic than the failure to include all known neurological detail (for a more detailed account see Grossberg, 1987)

Conclusions

Overall, connectionist modeling does indeed provide a forum for brain-style theorizing. However, the contact with neurophysiology appears to be “more apparent that real” (Quinlan, 1991). It should be pointed out again though, that the connectionists’ intention is to “offer a general and abstract model of computational architecture of the brain, to develop algorithms and procedures well-suited to this architecture and to explore them as hypotheses about the nature of the human information-processing system” (Rumelhart, 1989). On the other hand, “if our aim is to understand the brain, there is little value in designing and evaluating neural networks whose underlying assumptions about the brain organization are known at the outset to be false” (Crick, 1989).

Connectionists may have the details wrong but the important point for present purposes is that there is no further excuse for ignoring potential constraints on proposed cognitive architectures. As Crick (1989) has argued, if connectionists were to take the brain seriously then their models would end up being radically different to anything that has been developed to date. Fortunately, there seem to be many researchers in the connectionist movement who are trying to bring these systems closer to neural reality (Bates & Elman, 1993). They are heading in the right direction even though they have a long way to go.

REFERENCES

1. Barber, H.A. & Kutas, M. (2007). Interplay between computational models and electrophysiology in visual word recognition. Brain Research Reviews, 53(1): 98-123.
2. Bates, E.A. & Elman, J.L. (1993). Connectionism and the study of change. In M. Johnson (Ed.), Brain development and cognition: A reader. Blackwell Publishers: Oxford.
3. Berkeley, I.S.N. (1997). Some myths of connectionism. The University of Louisiana, Retrieved from http://www.ucs.louisiana.edu /isb9112/dept/phil341/myths/ myths.html, pp1-14.
4. Burton, A.M. & Young, A.W. (1999). Simulation and Explanation: Some harmony and some discord. Cognitive Neuropsychology, 16(1): 73-79.
5. Churchland, P.S. & Sejnowski, T. (1994). The computational brain. MIT Press: Cambridge, Mass.
6. Clark, A. (1989). Associative engines: connectionism, concepts and representational change. MIT Press: Cambridge, Mass.
7. Conrey, F.R. & Smith, E.R. (2007). Attitude representation: attitudes as patterns in a distributed, connectionist representational system. Social Cognition, 25(5): 718-735.
8. Crick, F.H.C. & Asanuma, C. (1986). Certain aspects of the anatomy and physiology of the cerebral cortex. In J.L. McClelland and D.E. Rumelhart (Eds.), Parallel distributed processing. Vol.2. Psychological and biological models. MIT Press: Cambridge, Mass.
9. Crick, F.H.C. (1989). The recent excitement about neural networks. Nature, 337: 129-32.
10. Decimone, R. & Ungerleider, L.G. (1989). Neural mechanisms of visual processing in monkeys. In F.Boller & J. Grafman (Eds.), Handbook of neurophysiology, Vol.2. Elsevier: Amsterdam.
11. Dreyfus, H. (1992). What computers still can’t do: A critique of artificial reason. MIT Press: Cambridge, Mass.
12. Engelbrecht, A.P. (2007). Computational intelligence: An introduction. Wiley & Sons Ltd: Chistester.
13. Feldman, J. & Ballard, D. (1982). Connectionist models and their properties. Cognitive Science, 6: 205-254.
14. Fodor, J. & Pylyshyn, Z. (1988). Connectionism and cognitive architecture: A critical analysis. Cognition, 28: 3-71.
15. Georgopoulos, A.P. (1990). Neurophysiology and reading. In M. Jeannerod (Ed.), Attention and performance, vol. 13. Lawrence Erlbaum Associates Inc: Hillsdale, NJ.
16. Gers, F. A., Schmidhuber, J. & Cummins, F. (2000). Learning to forget: Continual prediction with LSTM. Neural Computation, 12: 2451 - 2471.
17. Getting, P. (1989). Emerging principles governing the operation of neural networks. Annual Review of Neuroscience, 12: 184-204.
18. Grossberg, S. (1987). Competitive learning: from interactive activation to adaptive resonance. Cognitive Science, 11: 23-63.
19. Heinke, D. & Mavritsaki, E. (2009). Computational modeling in behavioural neuroscience: closing the gap between neurophysiology and behavior. Psychology Press: New York.
20. Hinton, G.E. & Anderson, J.A. (1989). Introduction to the updated edition. In G.E. Hinton & J.A. Anderson (Eds.), Parallel models of associative memory. Lawrence erlbaum associates: Hillsdale
21. Levine, D.S. (1991). Introduction to neural and cognitive modeling. Lawrence Erlbaum Associated: Hillsdale, NJ.
22. Maass, W., Legenstein, R. A. & Markram. H. (2002). A new approach towards vision suggested by biologically realistic neural microcircuit models. In H. H. Bueltho, S. W. Lee, T. A. Poggio & C. Wallraven. (Eds.), Biologically motivated computer vision, Proc. of the second international workshop, BMCV 2002, Tubingen, Germany, November 22-24, 2002, volume 2525 of lecture notes in computer science, pp. 282-293. Springer: Berlin.
23. McClelland, J.L. & Rogers, T.T. (2003). The parallel distributed processing approach to semantic cognition. Nature Reviews Neuroscience, 4: 310-322.
24. McLeod, P., Plunkett, K. & Rolls, E.T. (1998). Introduction to connectionist modeling of cognitive processes. Oxford University Press: Oxford
25. Monaghan, P., Arciuli, J. & Seva, N. (2008). Constraints for computational models of reading: evidence from learning lexical stress. In proceedings of the 30th Annual Conference of the Cognitive Science Society (pp. 457-462). Erlbaum: Mahwah, NJ.
26. Morris, R.G.M. (1989). Parallel distributed processing: implications for psychology and neurobiology. Clarendon Press: Oxford
27. O’Reilly, R.C. (1998). Six principles for biologically based computational models of cortical cognition. Trends in Cognitive Sciences, 11(2): 455-462.
28. O’Reilly, R.C. & Farah, M.J. (1999). Simulation and expla-nation in Neuropsychology and beyond. Cognitive neuropsychology, 16 (1): 49-72.
29. O’Reilly, R.C. & Frank, M.J. (2006). Making working memory work: a computational model of learning in the prefrontal cortex and basal ganglia. Neural Co-mputation, 18: 283-328.
30. O’Reilly, R. C. & Munakata, Y. (2000). Computational explorations in cognitive neuroscience: understa-nding the mind by simulating the brain. MIT Press: Cambridge, Mass.
31. Plaut, D.C., McClelland J.L., Seidenberg, M.S. & Patterson, K. (1996). Understanding normal and impaired word reading: computational principles in quasiregular domains. Psychological Review, 103; 56-115.
32. Poggio, T. (1988). M.I.T. progress in understanding images. In proceedings image understanding workshop, Cambridge, MA, April 1988. Morgan Kaufmann, San Mateo, CA.
33. Plaut, D. C. & McClelland, J. L. (2010). Postscript: parallel distributed processing in localist models without thresholds. Psychological Review, 117: 284–290.
34. Reid, S.J., Monroe, B.M., Brownstein, A.L., Gurveen Chopra, Y.Y. & Miller, L.C. (2010). A neural network model of the structure and dynamics of human personality. Psychological Review, 117(1): 61-92.
35. Roy, A. (2000). Artificial neural networks - a science in trouble. SIGKDD, 1(2): 33-38.
36. Rumelhart, D., McClelland, J. & the PDP Research Group (1986). Parallel distributed processing, MIT Press: Cambridge, Mass.
37. Rumelhart, D. (1989). The architecture of mind. In M. Posner (Ed.), Foundations of Cognitive Science, MIT Press: Cambridge, Mass.
38. Seidenberg, M.S. & Zevin, S.D. (2006). Connectionist models in developmental cognitive neuroscience: critical periods and the paradox of success. In Y. Munakata & M. Johnson (Eds.), Attention and performance XXI: Processes of change in brain and cognitive development. Oxford University Press: Oxford.
39. Smolensky, P. (1988). On the proper treatment of connectionism. Behavioural and Brain Sciences, 11: 1-74.
40. Sparks, D.L. & Mays, L.E. (1990). Signal transformations required for the generation of saccadic eye movements. Annual Review of Neuroscience, 13: 309-336.
41. Quinlan, P.T. (1991). Connectionism and psychology: A psychological perspective on new connectionist research. Harvester Wheatsheaf: London.
42. Winlow, W. (1990). Prologue; The “typical” Neuron. In W. Winlow (Ed.) neuronal communications, Manchester U.P: Manchester.
43. Πρωτόπαπας, Α. (2003/2004): Εισαγωγή στη θεωρία και μεθοδολογία των γνωσιακών επιστημών (σημειώσεις για μεταπτυχιακό μάθημα γνωσιακής επιστήμης). Τμήμα Μεθοδολογίας, Ιστορίας και Θεωρίας της Επιστήμης, Πανεπιστήμιο Αθηνών.